Introduction
If you have ever studied about probability and combinatorics in math at a high level, you must’ve probably come across the fact that the factorial of 0 equals 1. Like most people when I first heard about this, it didn’t make a whole lot of sense to me.
Today, my goal with this short blog post is to explain as to why this is the case.
Why the factorial of ‘nothing’ is 1.
A primer on factorials
The ‘!’ behind the 0, is notation for something called a ‘factorial’.
A factorial basically tells you to take the product of all integers and itself before it until you reach 1.
If that didn’t make any sense, take a look at this example.
1! = 1
2! = 1 x 2
3! = 1 x 2 x 3
4! = 1 x 2 x 3 x 4
See what I am talking about?
Now before we go to why 0! = 1, let’s take a look at something called exponents and some patterns in them which will help us later on.
𝑥ⁿ (read as “𝑥 to the power of n”) basically tells you that 𝑥 is multiplied by itself ‘n’ times, like:
2² = 2 x 2 = 4
2³ = 2 x 2 x 2 = 8
Now what do you think 2⁰ will be?
You might think that 2 multiplied by itself 0 times should be 0, but as it turns out any number to the power of 0 = 1.
2⁰ = 1, but how?
That might not make sense on first glance, but let me show you why it is correct.
Making sense out of all of this
Here’s a list of some of the powers of 2, you’ll notice a pattern over here.
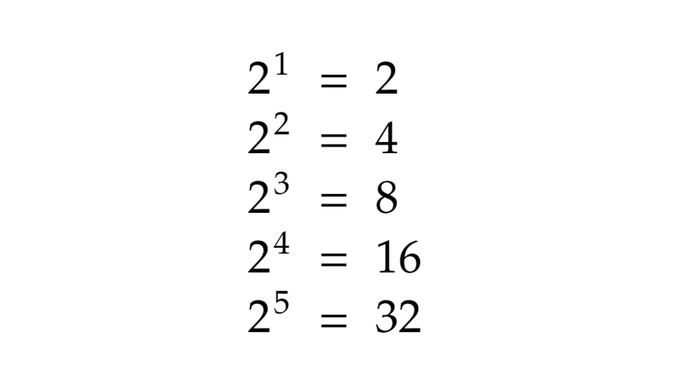
Each time you go up one level, you’re essentially dividing by 2, what happens when you get to 2⁰?
You get 1, and now it all makes sense.
This is why every number to the power of 0 is 1.
(This also works for powers in negative numbers)
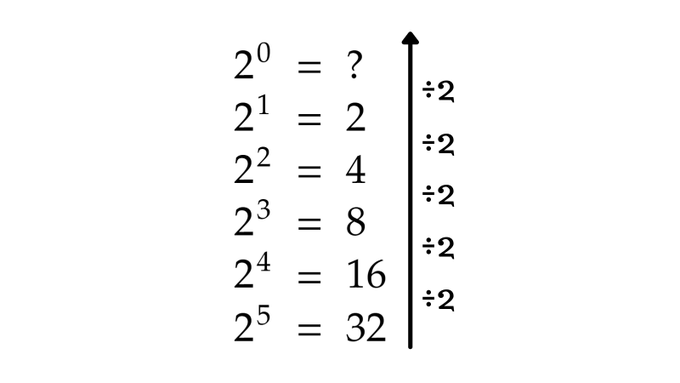
Factorials follow a similar pattern as you can see below, and as you can guess, 0! turns out to be 1 by this pattern!
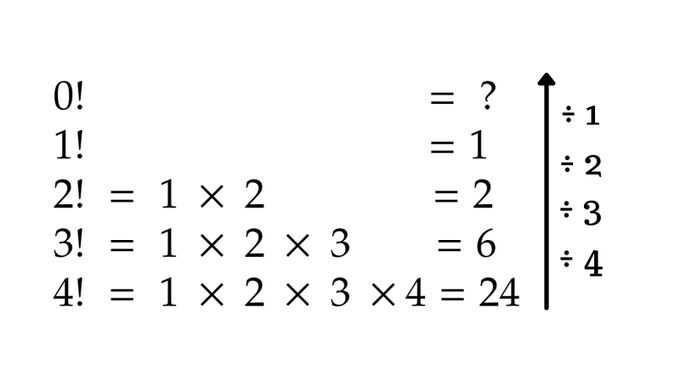
Factorials aren’t just about showing a neat pattern, they have real world use cases in combinatorics, a topic in math that deals with counting.
Let me explain.
Another explanation…
You have 2 balls, one yellow and the other is blue.
In how many different ways can you arrange them?

There are 2 possible cases, now similarly can you guess how many ways can you arrange 3 balls?
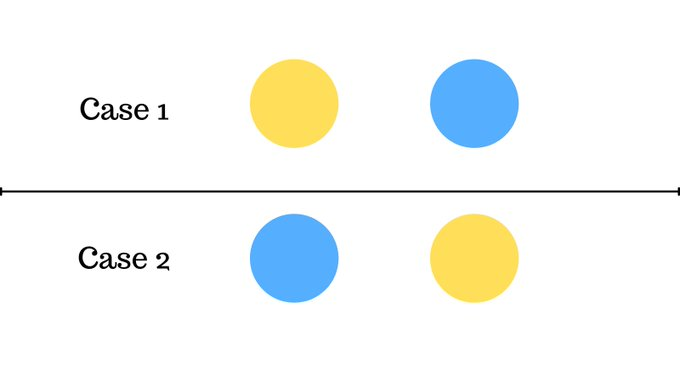
There are 6 possible cases to arrange 3 balls.

As it turns out, the number of ways you can arrange n balls is n!
2 balls = 2! = 2 3 balls = 3! = 6
2! basically means “in how many ways can arrange 2 balls” which is 2.
Now what 0! tells you is how many ways can you arrange 0 balls, or basically nothing.
There is exactly one way to show nothing!
Which again proves why 0! is 1.
